constexpr アルゴリズムの実装イディオムその１ - ボレロ村上

中３女子です。

今回は、constexpr におけるアルゴリズムの実装法について考える。

よく知られているように、constexpr 関数には言語規格上の制約が多くある。
ローカル変数が使えない、if や for などの制御構文が使えないなどは、C++11 に触れた者なら誰でも知っているだろう。
だが、それらは条件演算子や再帰によって、単純に代替できる問題である。
つまり、非 constexpr な実装に対して、処理の流れを本質的に変えることなく constexpr に書き換えることができる。

- 単純に書き換えられる例:

template<typename T>
T const& runtime_min(T const& a, T const& b) {
    if (b < a) return b;
    return a;
}

template<typename T>
constexpr T const& constexpr_min(T const& a, T const& b) {
    return b < a ? b
        : a
        ;
}

しかしながら、単純な書き換えでは解決できない問題もある。
例えばコンパイル時の再帰深度の制限などである。
そのため、constexpr でより良いアルゴリズムを実装するためには、ケースに応じたイディオムによって constexpr 特有の問題を解決する必要がある。

distance の実装

std::distance(first, last) は、[first, last) なるイテレータ間の距離を求める関数である。
典型的な実装は以下のようになる。

- std::distance

template<typename RandomAccessIterator>
typename std::iterator_traits<RandomAccessIterator>::difference_type
distance_impl(RandomAccessIterator first, RandomAccessIterator last, std::random_access_iterator_tag*) {
    return last - first;
}

template<typename InputIterator>
typename std::iterator_traits<InputIterator>::difference_type
distance_impl(InputIterator first, InputIterator last, void*) {
    typename std::iterator_traits<InputIterator>::difference_type n = 0;
    for (; first != last; ++first) {
        ++n;
    }
    return n;
}

template<typename InputIterator>
typename std::iterator_traits<InputIterator>::difference_type
distance(InputIterator first, InputIterator last) {
    typedef typename std::iterator_traits<InputIterator>::iterator_category* category;
    return distance_impl(first, last, category());
}

これを“単純に” constexpr に書き直すと、以下のようになる。

#include <sprout/iterator/next.hpp>

template<typename RandomAccessIterator>
constexpr typename std::iterator_traits<RandomAccessIterator>::difference_type
distance_impl(RandomAccessIterator first, RandomAccessIterator last, std::random_access_iterator_tag*) {
    return last - first;
}

template<typename InputIterator>
constexpr typename std::iterator_traits<InputIterator>::difference_type
distance_impl(InputIterator first, InputIterator last, void*) {
    return first == last ? 0
        : 1 + distance_impl(sprout::next(first), last, (void*)0)
        ;
}

template<typename InputIterator>
constexpr typename std::iterator_traits<InputIterator>::difference_type
distance(InputIterator first, InputIterator last) {
    typedef typename std::iterator_traits<InputIterator>::iterator_category* category;
    return distance_impl(first, last, category());
}

for を再帰で代替し、++ は sprout::next で代替する。
sprout::next は、次のような挙動をする。

1. iterator_next(it) が ADL callable であれば、それを呼ぶ。
2. それ以外で、ランダムアクセスイテレータかつリテラル型であれば、it + 1 を返す。
3. それ以外であれば、std::next(it) を返す。

このような仕様は、通常 ++ 演算子は副作用を持つため、副作用を持たない constexpr iterator_next を、イテレータの実装者が用意できるようにするためである。

これで distance を constexpr 化できただろうか？
残念ながら、この時点の実装には大きく二つの問題点がある。

問題1 : ポインタ同士の減算は定数式でない

第一の問題点は、コンパイル時にこの関数の引数にポインタを渡すと、コンパイルエラーになる。

static constexpr int arr[5] = {};
constexpr std::ptrdiff_t d = distance(arr, arr + 5); /* エラー！ */

なぜなら、ポインタ型はランダムアクセスイテレータとして扱われるが、C++11 においては、ポインタ同士の減算は定数式ではない。
そのため、コンパイル時に、ポインタ型での last - first を評価するとコンパイルエラーになる。

これを解決するには、ポインタ型も非ランダムアクセスイテレータと同じように処理するようにする。
つまり、SFINAE でポインタ型を Lookup から除外すればよい。

template<typename RandomAccessIterator>
constexpr typename std::enable_if<
    !std::is_pointer<RandomAccessIterator>::value,
    typename std::iterator_traits<RandomAccessIterator>::difference_type
>::type
distance_impl(RandomAccessIterator first, RandomAccessIterator last, std::random_access_iterator_tag*) {
    return last - first;
}

ちなみに、次期標準の C++1y では、ポインタ同士の減算も定数式として扱えるようになる予定である。

- See: 次期 C++ ではポインタ演算は定数式になるようだ／次期 C++ の constexpr 化を考える - ボレロ村上 - ENiyGmaA Code

問題2 : 再帰深度の制限

第二の問題点は、非ランダムアクセスかつ距離がコンパイラ定義の値（例えば 1024 だとか 512）を越えている場合、コンパイルエラーになる。

static constexpr int arr[5000] = {};
constexpr std::ptrdiff_t d = distance(arr, arr + 5000); /* エラー！ */

前述の実装では、距離をカウントアップする毎に再帰しているが、コンパイル時の constexpr 関数の再帰には深度制限があるからである。
すぐに深度制限を超えてしまうのは、この実装では、距離 N を求めるのに再帰深度 Ο(N) を必要とするからだ。
もし再帰深度が対数オーダー Ο(logN) などであれば、そう簡単には深度制限を越えることはないはずである。
では、対数オーダーの再帰はどのように実装するか？

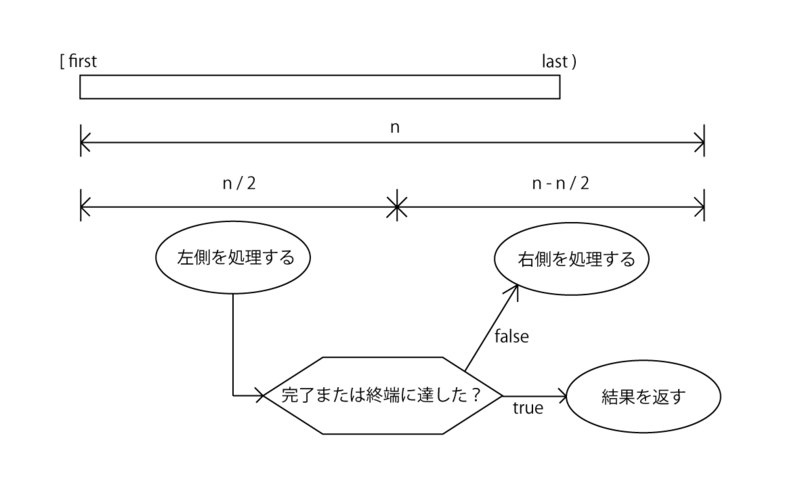
前提として、非ランダムアクセスな distance は、始端 first から順にカウントアップして終端 last に等しいイテレータを検索するアルゴリズムと捉えることができる。

まず、適当な検索範囲 n（n > 0）が与えられたと仮定する。（n >= N かもしれないし、n < N かもしれない）

1. 現在のイテレータが既に終端ならば、その時点のイテレータとカウントを返す。
2. 現在のイテレータが終端でなく、n == 1 ならば、カウントを 1 増やし、次のイテレータを返す。
3. 現在のイテレータが終端でなく、n > 1 ならば、n を左右二つに分けて再帰する。
  1. 左側をまず検索し、終端 last が見つかればその結果をそのまま返す。
  2. 左側に last が見つからなければ、次に右側を検索する。

上記を一つの処理単位とする。
マージソートのように範囲を二等分しながら処理するから、その再帰数は 2 の対数、つまり対数オーダーになる。

この処理単位について、

1. 検索範囲 n について終端 last が見つからなかった（n < N）場合は、次の範囲を続けて検索する。

というように再帰する。
このとき、次の検索範囲は前回の倍の n * 2 を選ぶようにする。
すると、n == 1 から始めて（n >= N）となるのに必要な再帰数もまた 2 の対数、つまり対数オーダーである。

対数オーダーの処理を合成した処理もまた対数オーダーであるから、全体としても対数オーダーになる。
以上をコードに落とすとこのような実装となる。

#include <sprout/utility/pair.hpp>

template<typename InputIterator>
constexpr sprout::pair<InputIterator, typename std::iterator_traits<InputIterator>::difference_type>
distance_impl_1(
    sprout::pair<InputIterator, typename std::iterator_traits<InputIterator>::difference_type> const& current,
    InputIterator last, typename std::iterator_traits<InputIterator>::difference_type n
    )
{
    typedef sprout::pair<InputIterator, typename std::iterator_traits<InputIterator>::difference_type> type;
    return current.first == last ? current
        : n == 1 ? type(sprout::next(current.first), current.second + 1)
        : distance_impl_1(
            distance_impl_1(
                current,
                last, n / 2     /* 左側を検索 */
                ),
            last, n - n / 2     /* 右側を検索 */
            )
        ;
}
template<typename InputIterator>
constexpr sprout::pair<InputIterator, typename std::iterator_traits<InputIterator>::difference_type>
distance_impl(
    sprout::pair<InputIterator, typename std::iterator_traits<InputIterator>::difference_type> const& current,
    InputIterator last, typename std::iterator_traits<InputIterator>::difference_type n
    )
{
    typedef sprout::pair<InputIterator, typename std::iterator_traits<InputIterator>::difference_type> type;
    return current.first == last ? current
        : distance_impl(
            distance_impl_1(
                current,
                last, n     /* 検索範囲 n を検索 */
                ),
            last, n * 2     /* 次の検索範囲 n * 2 を検索 */
            )
        ;
}
template<typename InputIterator>
constexpr typename std::iterator_traits<InputIterator>::difference_type
distance_impl(InputIterator first, InputIterator last, void*) {
    typedef sprout::pair<InputIterator, typename std::iterator_traits<InputIterator>::difference_type> type;
    return distance_impl(type(first, 0), last, 1).second;
}

pair を使っているのは、constexpr 関数では状態をローカル変数に保存できないため、
現在のイテレータとカウントを纏めて、引数と返値でやりとりするためである。

上記のような処理手順を呼出順に、より一般的に書くと、下記のようになる。

1. 処理完了するまで、処理範囲の長さ n を等倍しながら処理を再帰的に繰り返す。（手順 1）
2. 与えられた n の範囲を等分しながら、処理を再帰的に繰り返す。（手順 2）

もちろん、長さが既知である場合は、手順 1 は不要である。
ちなみに手順 2 の方法は、Sprout ライブラリでは、テイラー展開による数学関数の実装などにも用いられている。

このようなイディオムを使うことで、constexpr アルゴリズムについて、入力の長さ N に対して再帰深度 Ο(logN) の処理を書くことができる。
例えば検索（find, search 等）、カウント（const 等）、叙述（all_of 等）すべてに適用することができる。
アルゴリズム毎に合わせて考える必要があるが、概ね次の点を考えれば当てはめることができる。

1. 処理を完了する条件
2. 最小単位に対する処理
3. 必要な状態変数

中３女子ならば、アルゴリズムの効果と要件を見れば、自然にこのように問題を分解して考えることができる。

実際、Sprout ライブラリの STL 互換の（副作用のない）アルゴリズムはすべてこのような実装になっている。

- See: Sprout/sprout/algorithm at master · bolero-MURAKAMI/Sprout · GitHub

ゆえに、副作用のない STL アルゴリズムはすべて、高々再帰深度 Ο(logN) で constexpr 化できることが実証されている。
このように、constexpr 特有の問題であっても、とても明快でわかりやすいイディオムで解決することができる。

次回は、定数式においてポインタを効率的にイテレータとして用いる方法について書こうと思う。